Skip to main content

Quadtree Cheatsheet

Patrick Cozzi

In geospatial apps, quadtrees are widely used for streaming imagery, terrain, vectors, and other data. Here’s a cheatsheet for some common operations for a complete quadtree (all leaf tiles are at the same level). We use the term tile, instead of node, since tile is popular in the geospatial world, and use the term level to define the zero-based depth/scale/zoom-level/z of a tile. The root is at level zero, its children are at level one, and so on.

Number of tiles at a level

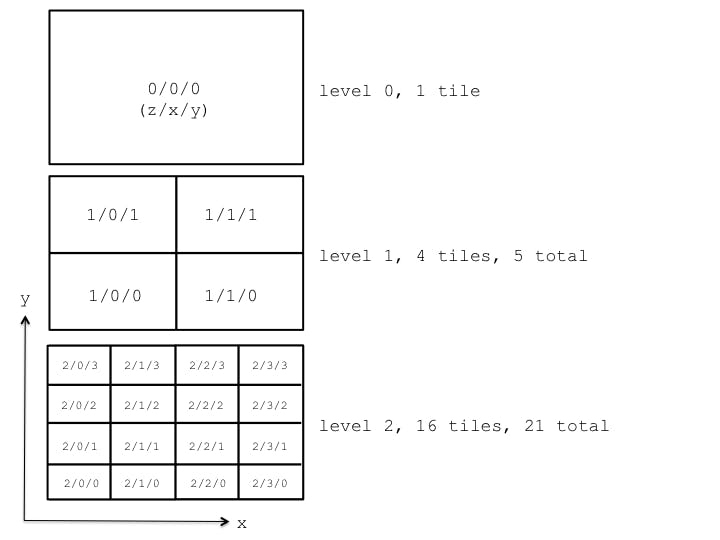
Each quadtree tile is split into four tiles by two axis-aligned splitting-planes so at a level n, there are 2^n by 2^n tiles in the level, or just 4^n.

function numberOfTiles(n) {
   return Math.pow(4, n);
}

// numberOfTiles(0) -> 1
// numberOfTiles(1) -> 4
// numberOfTiles(2) -> 16

Total number of tiles up to a level

Above, we compute the number of tiles at a level. Let’s extend this to also include all of the ancestor tiles up to and including the root. This is the sum of 4^n for n from zero to the maximum level, n.

function numberOfTotalTiles(n) {
   return (Math.pow(4, n + 1) - 1) / 3;
}

// numberOfTotalTiles(0) -> 1
// numberOfTotalTiles(1) -> 5 (4 + 1)
// numberOfTotalTiles(2) -> 21 (16 + 4 + 1)

Maximum level for a number of leaf tiles

.

To build a quadtree that will accommodate m leaf tiles (where m is greater than zero), take the ceiling of the log of m base 4

function maximumLevel(m) {
   return Math.ceil(Math.log(m) / Math.log(4.0));
}

// maximumLevel(1)  -> 0
// maximumLevel(2)  -> 1
// maximumLevel(4)  -> 1
// maximumLevel(5)  -> 2
// maximumLevel(16) -> 2

Tile Map Service (TMS) Layout

In geospatial apps, Tile Map Service (TMS) and similar layouts are widely used for requesting quadtree tiles.

Generally, the quadtree is subdivided by lines of longitude (x) and latitude (y). The path for a quadtree tile is z/x/y.png (.png could be any extension), where z is the level, x increases from west to east, and y increases from south to north. For example, 0/0/0.png is the root tile; 1/0/0.png is the bottom-left tile at level 1; and 1/0/1.png is the top-left tile at level 1.